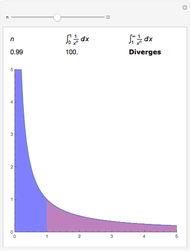
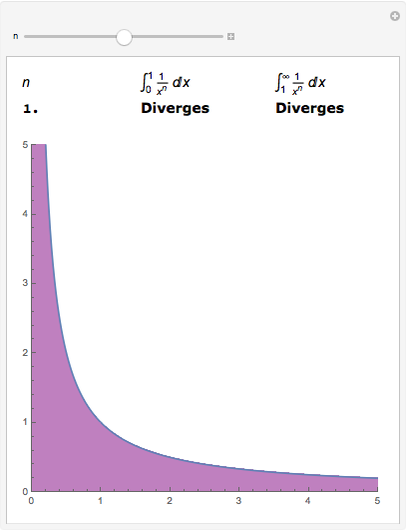
Recall the important classes of improper integrals we examined in Section5.10. to the improper integral being convergent or divergent.
#IMPROPERINTEGRALS NOTEA HOW TO#
In the previous section, we learned how to compute improper integrals - integrals involving certain functions over unbounded integrals, as well as functions that become infinite at a point within or at the endpoint of the interval of integration. If the value of an improper integral is a finite number, as in this example, we say that the integral converges, and if not we say that the integral diverges. When can the convergence behavior of one improper integral be used to determine the convergence behavior of another improper integral? What are some typical improper integrals that we can classify as convergent or divergent? Section 5.11 Comparison of Improper Integrals Motivating Questions
Population Growth and the Logistic Equation. Qualitative Behavior of Solutions to DEs. An Introduction to Differential Equations. Physics Applications: Work, Force, and Pressure. Area and Arc Length in Polar Coordinates. The following figures show an examples of a graph of functions. Using Definite Integrals to Find Volume by Rotation and Arc Length The extended integrals are now called improper integrals. Using Definite Integrals to Find Area and Volume. 
Using Technology and Tables to Evaluate Integrals. Use the Comparison Test to determine if the following integrals converge or diverge. The Second Fundamental Theorem of Calculus Section 1-9 : Comparison Test for Improper Integrals. Constructing Accurate Graphs of Antiderivatives. Determining Distance Traveled from Velocity. Using Derivatives to Describe Families of Functions. Using Derivatives to Identify Extreme Values. Derivatives of Functions Given Implicitly. Derivatives of Other Trigonometric Functions. Interpreting, Estimating, and Using the Derivative We say an improper integral is convergent if the corresponding limit exists, and divergent if the limit does not exist. Improper integrals of Type I are integrals of continuous functions on infinite domains. The Derivative of a Function at a Point Review: Improper integrals type I and II.
0 kommentar(er)
